Komplexe Zahlen

Komplexe Zahlen	Eine kurze Einführung. Auf Vollständigkeit wird verzichtet. Beweise fehlen. Es geht allein darum, einen schnellen Überblick zu gewinnen. Die komplexen Zahlen werden an dieser Stelle hauptsächlich vorgestellt, weil man sie zum Verständnis der Fast Fourier Transformation (FFT) benötigt.
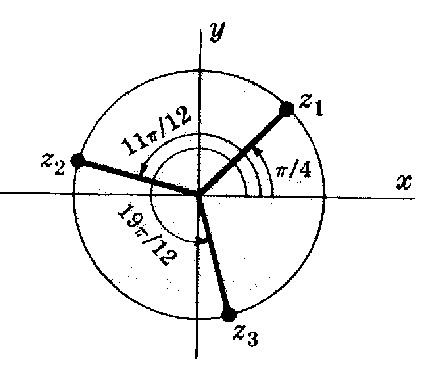
Darstellung:	Eine Zahl z = x+iy mit den reellen Zahlen x und y heißt komplexe Zahl, wenn i² = -1 ist. x heißt Realteil und y Imagionärteil der komplexen Zahl z. Regel: rechne mit solchen Zahlen wie gewohnt, berücksichtige dabei aber i² = -1. Gaußsche Zahlen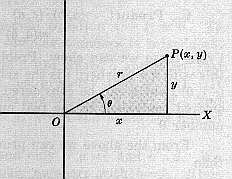ebene: Der Abstand des Punktes in der Gaußschen Zahlenebene vom Urspruch ist für den Winkel q gilt Aus z =x + iy wird mit x = r cos(q) und y = r sin(q): z = r (cos(q)+ i sin(q))
Euler, Leonhard (1707-1783;76) Reihenentwicklung, Eulersche Gleichung eⁱ^p=-1	Man kann zeigen, dass man sin- und cos- und exp-Funktion in Potenzreihen entwickeln kann. (siehe dazu Taylorreihe) Ersetzt man in e^x die Größe x durch ix so erkennt man, dass sich e^x. als schreiben läßt. und mit x = p haben wir eⁱ^p=-1 Gleichzeitig haben wir eine dritte Darstellung gefunden: z = x + iy = r(cos(q) + isin(q)) = reⁱ^q.
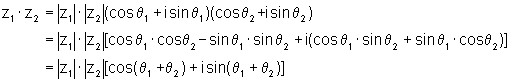
Rechenregeln	Die zu z konjugiert komplexe Zahl: der Betrag einer komplexen Zahl: die Summe zweier komplexen Zahlen: das Produkt zweier komplexer Zahlen: Wählt man zur Produktbildung die Darstellung z = r(cos(q) + isin(q)) dann vereinfacht sicht das Produkt: bzw. (mit der Darstellung Z= reⁱ^q: Grafisch läßt sich die Multiplikation als Drehung eines Punktes um den Ursprung verstehen. 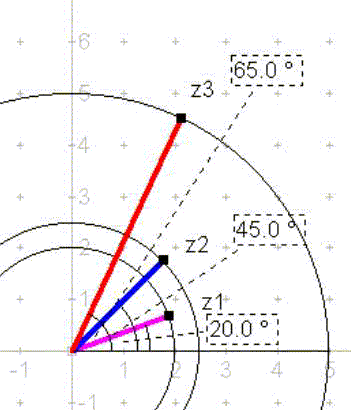Die nebenstehende Zeichnung veranschaulicht dies: Der Punkt, der z₁ darstellt, ist um 20⁰ von der pos. x-Achse gedreht. der Punkt der z₂ darstellt um 45⁰. Somit muss der Punkt, der das Produkt z₃ veranschaulicht, um 20⁰+45⁰ = 65⁰ gedreht sein. Die Entfernung des "Produktpunktes" vom Ursprung ist das Produkt der Entfernungen von z₁ und z₂ vom Ursprung. Produkte von komplexen Zahlen, deren Beträge 1 sind, liegen selbst wieder auf dem Einheitskreis. Für die Division ist die Formel ähnlich einfach. Die geometrische Interpretation läßt sich leicht finden. Die dargestellte Zeichnung veranschaulicht dann die Division z₃ / z₂ = z₁ oder aber auch z₃/z₂ = z₁. 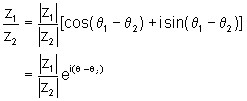Für das Potenzieren gilt dann: Für die Wurzel haben wir:
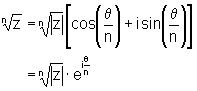
Die Gleichung zⁿ = w	Bei der Gleichung zⁿ = w beschränken wir uns zunächst auf solche komplexe Zahlen, deren Betrag 1 ist. Eine Veranllegmeinerung ist dann nicht mehr schwer. Sicherlich ist Lösung, aber ist es die einzige? Im reellen hat die Gleichung x² = 1 auch die Lösung x = 1 aber es nicht die einzige, auch x = -1 löst die Gleichung. Tatsächlich gibt es für unser Problem n Lösungen: Durch Potenzieren mit n prüfe man nach, dass wir für jedes zugelassene k wieder die Darstellung von w bekommen. Würde man übrigens k weiterlaufen lassen, käme man zu keiner weiteren Lösung. Wegen der Periodizität der sin- und cos- Funktionen wiederholen sich die Lösungen.
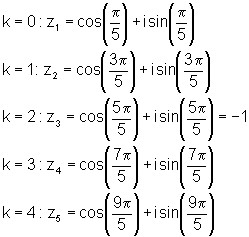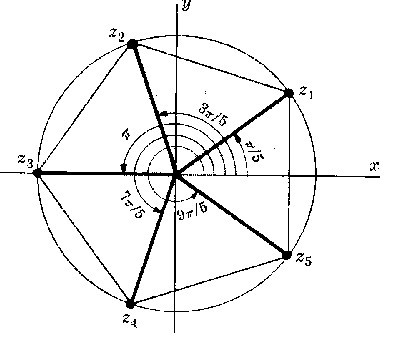
Beispiel z⁵ = -1	; Allgemeine Lösung: Die einzelnen Lösungen sind dann: Die grafische Darstellung der Lösungen
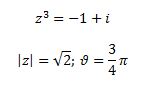
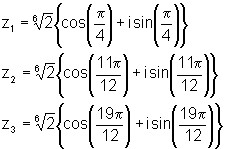
Beispiel z³ = -1+i	Allgemeine Lösung: Die Lösungen im einzelnen: Die grafische Darstellung der Lösungen (Die Lösungen liegen jetzt auf einem Kreis mit dem Radius: )
(c) Pohlig