Euklidscher Algorithmus

13.2 Der Euklidsche Algorithmus

Der Algorithmus

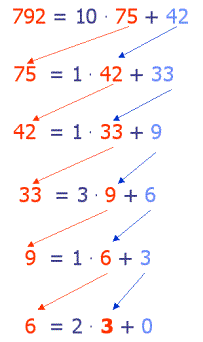Das Beispiel zeigt, wie man mit Hilfe des Euklidschen Algorithmus' den ggT(792,75) bestimmt.

Im ersten Schritt fragen wir, wie häufig die zweite Zahl, also 75 ganzzahlig in der ersten, nämlich 792 enthalten ist. Diese Ganzzahldivision liefert 10 und den Rest 42. Im weiteren Verlauf werden wir sehen, dass die Zahl 10 für den weiteren Verlauf unwichtig ist, also getrost vergessen werden kann. Wesentlich ist, wir berechnen 792 mod 75 und das ist 42. Im zweiten Schritt fragen wir: Wie groß ist der Rest, wenn wir 75 ganzzahlig durch 42 teilen. Wir bestimmen also 75 mod 42. Diese Schritte wiederholen sich

Somit berechnen wir nacheinander:

792 mod 75 = 42
75 mod 42 = 33
42 mod 33 = 9
33 mod 9 = 6
9 mod 6 = 3
6 mod 3 = 0

Ist der Rest 0, ist der Algorithmus zu Ende. 3 ist der gesuchte größte gemeinsame Teiler. Da garantiert werden kann, dass der Rest irgendwann 0 ist, sagen wir, der Algorithmus terminiert.

Nach dieser Untersuchung am Beispiel, formulieren wir den Algorithmus allgemein, so dass wir schließlich in Java implementieren können. Auf den Beweis des Algorithmus' verzichten wir und verweisen auf die einschlägige Literatur verwiesen.

allgemeine Darstellung Zu bestimmen ist ggT(a,b)
Wir setzen r₀=a und r₁ = b; und bestimmen

1. Schritt	r₀ mod r₁ =: r₂
2. Schritt	r₁ mod r₂ =: r₃
3. Schritt	r₂ mod r₃ =: r₄
i-ter Schritt	r_i-1 mod r_i =: r_i+1
n-ter und letzter Schritt. Er ist dadurch gekennzeichnet, dass der Rest 0 ist.	r_n-1 mod r_n = 0 r_n ist der gesuchte ggT(a,b)

Der Java-Code

int r;
do {
r = a%b;
a = b;
b = r;
} while(b!=0);
//a ist der ggT

Der ggT(a,b) wird bestimmt. Wir verwenden eine do-while-Schleife und vermeiden so eine Initialisierung von r.
r = a%b; realisiert r_i-1 mod r_i =: r_i+1 wobei das i den Schleifendurchgang mitzählt, was im Programm natürlich überflüssig ist. Nachdem der Rest berechnet wurde. Wird in den nächsten beiden Zeilen a = b; und b = r; der nächste Schleifendurchgang vorbereitet, d.h. r_i "rutscht" vor mod und der Rest hinter mod. Diese Vorbereitung geschieht auch dann, wenn sie eigentlich nicht mehr nötig ist, im letzten Durchgang, wenn der Rest 0 ist, deshalb ist der gesuchte ggT in a und nicht wie man im ersten Moment vermuten möchte in b.

Download:
GgT3.java

import info1.*;
public class GgT3{
   public static void main(String[] args){
      StoppUhr eineStoppUhr = new StoppUhr();
      int ggT = 1;
      System.out.print("erste Zahl: ");
      int a = Console.in.readInt();
      System.out.print("zweite Zahl: ");
      int b = Console.in.readInt();
      eineStoppUhr.starten();
      int r;                         //1
      do{
         r = a%b;
         a = b;
         b = r;
      } while(b!=0);
      eineStoppUhr.stoppen();
      ggT = a;
      System.out.println(ggT);
      System.out.println(eineStoppUhr);
   }
}

Kommentar zu Zeile //1:
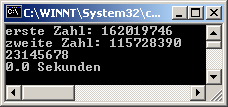
die Variable r braucht vor einer do..while-Schleife nicht initialisiert zu werden, wenn dies im Schleifenrumpf passiert. Denn eine Schleife dieses Typs wird mindestens einmal durchlaufen und r bekommt mit r = a%b einen Wert garantiert bekommt.

Ergebnis

Da die StoppUhr, wie ein Blick in ihren Quelltext verrät, auf Millisekunden genau die Zeit stoppt, ist die Laufzeit von 16,543 Sekunden auf unter 0,001 Sekunden geschrumpft.

zu 13.3 Der ggT rekursiv definiert.

zur Startseite www.pohlig.de (C) MPohlig 2003