16.5 Koch-Kurve
 
Selbst- ähnlichkeit

Fraktale

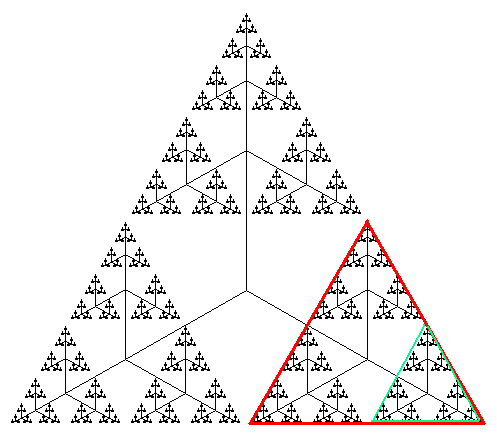
 Schon beim Sierpinski-Dreieck ist uns eine Figur begegnet, die zu sich selbst ähnlich ist. Wenn man davon absieht, dass beim Implementieren und dann beim Zeichnen es eine Grenze der Darstellung geben muss, im ersten Fall würde es ohne den Rekursionsausstieg einen endlosen Rekursionsaufruf geben, und im zweiten Fall kommt man die Grenzen der grafischen Darstellung, kann man einen Teil der Figur herausgreifen und man erhält in diesem Teil wieder das Ganze. Selbstähnliche Figuren nennt man auch Fraktale1).

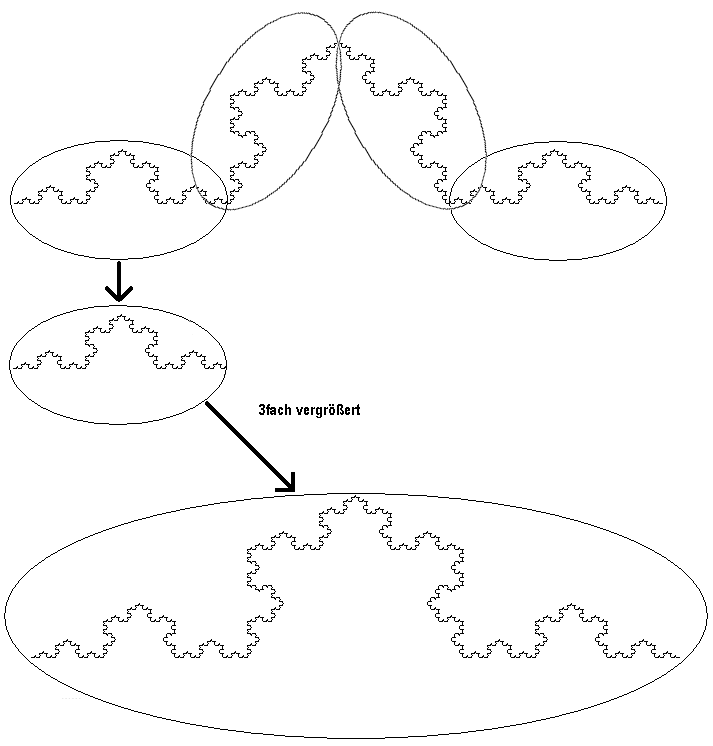
Stellt man sich ein idealisiertes Sierpinski-Dreieck vor, d.h. es gibt eine beliebige Zeichengenauiogkeit und die Rekursionstiefe sei unendlich, dann kann man das grün umrandete Dreieck auf die Größe des rot umrandeten zoomen und es ist vom rot umrandeten nicht zu unterscheiden.  Es gibt auch Kurven (auch Streckenzüge), die über die gleiche Eigenschaft verfügen. Sie haben, wieder in idealisierter Darstellung, eine besondere Eigenschaft: Sie sind innerhalb eines begrenzten Flächenbereichs eine unendliche Länge. Eine Vertreterin solcher Kurven wollen wir kennen lernen. Es ist die Kochkurve.

 
Koch-Kurve Wir geben eine Strecke vor.
  Wir dritteln die Strecke und setzten ein Dreieck nach der folgenden Vorschrift darauf: Gehe um die neue Strecke nach vorne (F = forward), drehe um a = 60 gegen den Urzeigersinn (+), gehe wieder um vorwärts, drehe zweimal um a mit dem Uhrzeigersinn (- -), gehe vorwärts, drehe um a gegen den Uhrzeigersin und gehe ein letztes Mal vorwärts. Wir können mit der F,+, - Notation also kurz schreiben:

L := F + F - - F + F

Das L-System in Java:

t.vor(l);          //F
t.rechts(-60);     //+
t.vor(l);          //F
t.rechts(120);     //--
t.vor(l);          //F
t.rechts(-60);     //+
t.vor(l);          //F

Wir erhalten dann die nachstehende Figur:
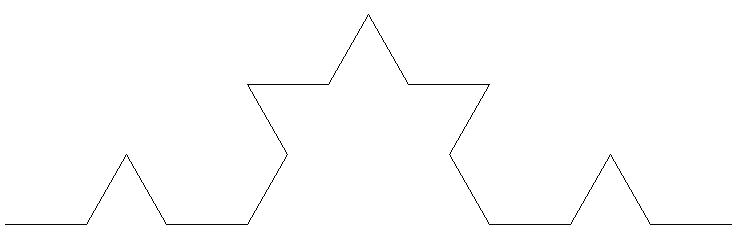
nächste Stufe Auf jeder Strecke machen wir nach einer weiteren Drittelung der Strecke das gleiche wieder. Das heißt jedes F ersetzen wir durch L mit einer Drittelung der Strecke:

L  + L -- L + L mit L = F + F - - F + F

wir erhalten dann:

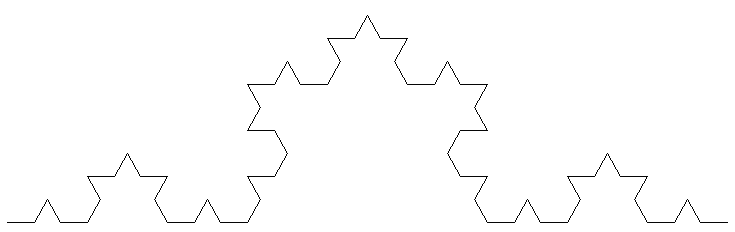
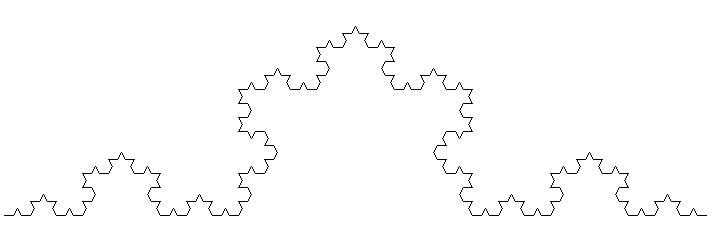
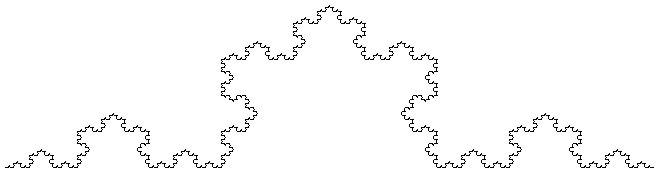
nöchste Stufen wir ersetzen L erneut durch L und dritteln zuvor wieder die Strecke, u.s.w


 
   

Auch die Kochkurve ist selbstähnlich, wie die nachstehende Grafik veranschaulicht.
 
der rekursive Aufruf in Java 
zeichne(t,l/3);    //L
t.rechts(-60);     //+
zeichne(t,l/3);    //L
t.rechts(120);     //--
zeichne(t,l/3);    //L
t.rechts(-60);     //+
zeichne(t,l/3);    //L
Die rekursive Methode zeichne() in der Klasse KochKurve. java Die Kochkurve können wir zeichnen, wenn wir die Folge L + L - - L + L in einer rekursiven Methode unterbringen, wobei wir den Abbruch der Rekursion durch das tatsächliche Vorwärtsschreiten geschieht, wenn die Schrittlänge einen bestimmten Wert unterschritten hat.
public class KochKurve{
   public void zeichne (Turtle t, int l){
      if (l<9){
          t.vor(l);
      }
      else{
         zeichne(t,l/3);    //L
         t.rechts(-60);     //+
         zeichne(t,l/3);    //L
         t.rechts(120);     //--
         zeichne(t,l/3);    //L
         t.rechts(-60);     //+
         zeichne(t,l/3);    //L
      }
   }
}
Downloads:

 KochKurve. java

KochKurve Demo.java

Turtle.class		 Das Verändern der GUI für die Kochkurve ist einfach und wird hier nicht mehr dargestellt (Anmerkung: Sie müssen zusätzlich die Fenstergröße anpassen). Zum Testen müssen dann die Bytecodes von KochKurve.java und KochKurveDemo.java sowie Turtle.class in einem gemeinsamen Verzeichnis liegen.
Übung Schreiben Sie eine neue Kochkurve mit dem L-System:

L := F + F - F -  F + F, mit a = 900 und der Bedingung, dass beim rekursiven Aufruf die Streckenlänge wieder gedrittelt wird.
   
Fußnoten  

1)

 Das Wort Fraktale kommt aus dem lateinischen und bedeutet gebrochen. Man erinnere sich, dass man in der Medizin einen Knochenbruch auch häufig als eine Knochenfraktur bezeichnet. Was ist aber in der Figur gebrochen? Es ist die Dimension. Das zu begründen würde hier zu weit führen. Es sei hier z. B. auf das leider nicht mehr lieferbare Buch

Pleitgen e.a - Beustein des Chaos. Fraktale
Broschiert - Rowohlt Tb.
Erscheinungsdatum: 1998
ISBN: 3499602504


Pleitgen  e.a - Chaos. Bausteine der Ordnung
Broschiert - Rowohlt Tb.
Erscheinungsdatum: 1998
ISBN: 3499605511

 
zu 16.6 Noch eine Kochkurve
zur Startseite www.pohlig.de  (C) MPohlig 2003