| 16.7
Pythagoras Baum |
|
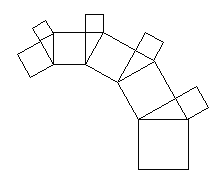
| Erste Stufe | In der
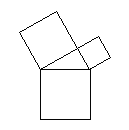
ersten Stufe hat der Pythagoras-Baum die folgende Gestalt:
Man gibt ein Quadrat mit einer
bestimmten Seitenlänge vor. Über der einen Seite zeichnet man ein
rechtwinkliges Dreieck (in unserem Beispiel hat dieses die Winkel 300
und 600). Über die noch freien Katheten zeichnet man die
Kathetenquadrate. Es entsteht die bekannte Darstellung zum Pythagoräischen
Lehrsatz. Den Pythagoras-Baum erhält man nun, wenn man die
Kathetenquadrate selbst wieder als Hypothenusenquadrate für die nächste
Generation auffasst. Wir erhalten dann das nächste Bild.
|
Es
handelt sich in unseren Darstellungen noch nicht um den Pythagoras-Baum,
Den erhalten wir erst, wenn wir die Darstellung idealisieren, genauer,
wenn wir uns die Rekursionstiefe unendlich "vorstellen".
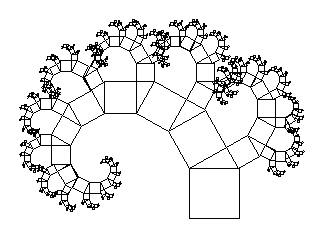 Einen Eindruck
von der Figur bekommen wir, wenn wir die (in Programmen immer endlichen)
Rekursionstiefe sehr groß machen, z.B. so, dass erst dann keine weitere
Generationen erzeugt werden, wenn die Seitenlönge des linken Quadrats ein
Pixel unterschreiten würde. Kommen wir also zu der Frage, wie
programmieren wir die Methode
zeichnen() in der Klasse
Pythagoras-Baum? Einen Eindruck
von der Figur bekommen wir, wenn wir die (in Programmen immer endlichen)
Rekursionstiefe sehr groß machen, z.B. so, dass erst dann keine weitere
Generationen erzeugt werden, wenn die Seitenlönge des linken Quadrats ein
Pixel unterschreiten würde. Kommen wir also zu der Frage, wie
programmieren wir die Methode
zeichnen() in der Klasse
Pythagoras-Baum? |
|
| Der Algorithmus |
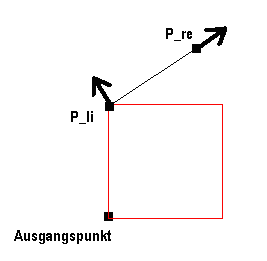 Die
Methode zeichne()
in Umgangssprache: Die Turtle sitze im
Ausgangs-punkt. Zuerst wir ein Quadrat gezeichnet. Danach bewegt sich die
Turtle auf den Punkt P_li, dreht ihre Blickrichtung um 300 nach
links (der dicke Pfeil gibt die Blickrichtung der Turtle an). Dann erfolgt
der rekursive Aufruf der Methode
zeichne(). Die Turtle bewegt
sich mit neuer Blickrichtung in den Punkt P_re. Wieder der rekursive
Aufruf der Methode zeichne(). Schließlich wird die Turle wieder in den
Ausgangspunkt gesetzt. Eine wichtige Anmerkung: Das Bewegen zu den
Punkten P_li und P_re geht immer vom Ausgangspunkt aus, wohin die Turtle
zunächst gesetzt werden muss. Der Grund dafür ist, die manglnde
Genauigkeit beim Zeichnen, wenn man die Bewegungen alleiun mit den
Turtle-Methoden vor(..)
und rechts(..)
bewerkstelligt. Die Ungenauigkeit schaukelt sich mit zunehmender
Rekursionstiefe immer höher, so dass die rechtwinklige Dreiecke nicht mehr
geschlossen erscheinen. Die
Methode zeichne()
in Umgangssprache: Die Turtle sitze im
Ausgangs-punkt. Zuerst wir ein Quadrat gezeichnet. Danach bewegt sich die
Turtle auf den Punkt P_li, dreht ihre Blickrichtung um 300 nach
links (der dicke Pfeil gibt die Blickrichtung der Turtle an). Dann erfolgt
der rekursive Aufruf der Methode
zeichne(). Die Turtle bewegt
sich mit neuer Blickrichtung in den Punkt P_re. Wieder der rekursive
Aufruf der Methode zeichne(). Schließlich wird die Turle wieder in den
Ausgangspunkt gesetzt. Eine wichtige Anmerkung: Das Bewegen zu den
Punkten P_li und P_re geht immer vom Ausgangspunkt aus, wohin die Turtle
zunächst gesetzt werden muss. Der Grund dafür ist, die manglnde
Genauigkeit beim Zeichnen, wenn man die Bewegungen alleiun mit den
Turtle-Methoden vor(..)
und rechts(..)
bewerkstelligt. Die Ungenauigkeit schaukelt sich mit zunehmender
Rekursionstiefe immer höher, so dass die rechtwinklige Dreiecke nicht mehr
geschlossen erscheinen. |
| Die Klasse Pythagoras Baum.java |
|
|
Downloads: |
Turtle.class PythagorasBaum.java PythagorasBaumDemo. java |
| zu den | Hausaufgaben |
| zur Startseite | www.pohlig.de (C) MPohlig 2003 |
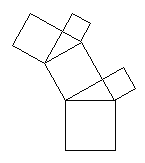 Wichtig ist
anzumerken, dass das kleinere Kathetenquadrat keine nachfolgende
Generation erzeugt, da seine Länge die Abbruchbedingung der Rekursion
erreicht. Die Abbruchbedingung wird über die Seitenlänge des linken
Kathetenquadrats festgelegt. Setzten wir diese niedriger, erhöhen wir die
Rekursionstiefe. Die nächste Generationen lieferen aber immer noch nur
weitere Generationen für das linke Kathetenquadrat. Erst wenn die
Rekursionstiefe genügend groß ist, erscheinen in der grafischen
Darstellung auch Nachfolgegenerationen für die rechten Kathetenquadrate:
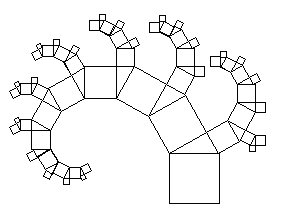
Wichtig ist
anzumerken, dass das kleinere Kathetenquadrat keine nachfolgende
Generation erzeugt, da seine Länge die Abbruchbedingung der Rekursion
erreicht. Die Abbruchbedingung wird über die Seitenlänge des linken
Kathetenquadrats festgelegt. Setzten wir diese niedriger, erhöhen wir die
Rekursionstiefe. Die nächste Generationen lieferen aber immer noch nur
weitere Generationen für das linke Kathetenquadrat. Erst wenn die
Rekursionstiefe genügend groß ist, erscheinen in der grafischen
Darstellung auch Nachfolgegenerationen für die rechten Kathetenquadrate: