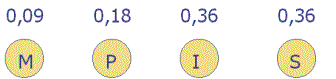H(M)= 0.09
H(P) = 0.18
H(I) = 0.36
H(S) = 0.36

Nun weicht man von der üblichen Kodierung der Zeichen ab. Solche, die häufiger vorkommen, bekommen einen Kode, der im Speicher weniger Platz  belegen als Zeichen, die weniger häufig vorkommen. In folgendem Kode sind diese Forderungen erfüllt. 

Code(M) = 100
Code(P) = 101
Code(I) = 11
Code(S) = 0

Die Zeichenkette "MISSISSIPPI" lässt sich dann wesentlich kürzer codieren:

Code(MISSISSIPPI) = 100110011001110110111

die unterschiedliche Färbung zeigt, zu welchen Buchstaben sie gehören, genauer, jedes mal wenn sich die Farbe ändert, beginnt ein neues Zeichen.  

Durch Abzählen findet man, dass die Datenmenge der Zeichenkette jetzt nur noch 21 bit hat, eine Kompression auf ca. 23,9% der ursprünglichen Datenmenge. 

Drei Fragen stellen sich. 

• Wie findet man den neuen Kode, 
• warum wählt man gerade den aufgezeigten Kode und keinen anderen und schließlich. Warum also nicht 
  Code(S)=0, 
  Code(I)=1, 
  Code(P)=01 und 
  Code(M)=10?
  Die Komprimierung wäre sicherlich noch effektiver. Es zeigt sich nun, dass dann der Kode noch weniger bit beinhaltet, das Komprimieren und Dekomprimieren aber ineffizienter wird. Und schließlich
• wie wird decodiert, wie erkennt also der Rechner wann ein neues Zeichen kommt. Die Problematik der letzten Aufgabe wird durch Weglassen der Farben im Kode deutlich.  Wie lässt sich also 100110011001110110111 wieder zu MISSISSIPPI decodieren?

Die Antworten auf diese drei Fragen findet wir im Huffman-Algorithmus, der an unserem Beispiel "MISSISSIPPI" aufgezeigt wird

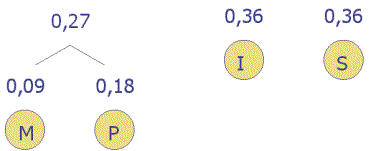
Im ersten Schritt werden die Zeichen sortiert nach der rel. Häufigkeiten ihres Auftretens im zu komprimierenden Text aufgeschrieben:

Man sucht sich die zwei Häufigkeiten heraus, die die kleinste Summe bilden, das wären 0,09 + 0,18 = 0,27. Es ist dies immer die Summe der ersten beiden Glieder. Die Summe ersetzt die beiden Summanden samt ihren Zeichen, die unter die 0,27 gestellt werden. Diese Summe wird dann wieder in die Reihe so eingeordnet, dass die Sortierung nach der Häufigkeit erhalten bleibt.

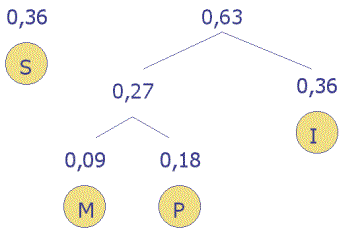
Der zweite Schritt des Algorithmus wird nun wiederholt: Die Summanden, die jetzt die kleinste Summe bilden, sind 0,27 und 0,36, ihre Summe ist 0,63. Ihre Zusammenfassung und ergibt nach dem Neuordnen den folgenden Baum.:

Der letzte Schritt ist erreicht, wenn alle Zeichen in den Baum eingefügt sind..

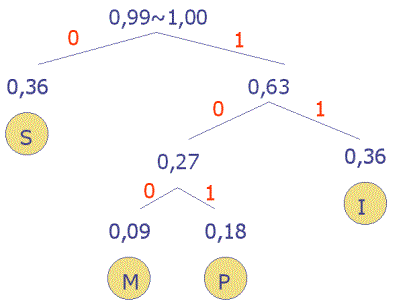
Dieser Baum zeichnet sich dadurch aus, dass in der sog. Wurzel immer die 1, und in einem Knoten immer eine Zahl steht, die die Summe ihrer Konten darunter ist. Die Verbindungslinien von Knoten zu Knoten nennt man die Kanten des Baumes. Nach links - unten weisende Kanten bekommen den Wert 0, die nach rechts - unten weisenden den Wert 1.  An den Enden des Baumes, man nennt diese Knoten auch Blätter, stehen dann die Zeichen. So erreicht man den Buchstaben P wenn man dem Pfad 1-0-1 folgt. Wir geben deshalb dem Buchstaben P den Kode Code(P)=101. Der Algorithmus, der den Baum aufbaut ist einfach, denn, wie wir gesehen haben, wird beim Einfügen eines neuen Elementes der Baum nur ergänzt aber nicht umstrukturiert. 

Ein Blick auf den Baum zeigt auch: wenn man einen Text mit mehr als zwei Zeichen codieren will, können die 0 und 1 nicht gleichzeitig vergeben werden, sondern nur die 1 oder die 0, da an mindestens einem der beiden Kantenenden der Restbaum angehängt ist. Diese Tatsache beantwortet die Frage, warum wir für den Text MISSISSIPPI den  Code(S)=0, Code(I)=1, Code(P)=01 und Code(M)=10 nicht wählen können, denn sonst könnten wir den Baum und seine Struktur nicht mehr nützen. Aber darauf wollen wir nicht verzichten, warum, das zeigt die folgenden Überlegungen:
Haben wir beim der ersten Schritt des Algorithmus, die Buchstaben entsprechend ihrer Häufigkeitserteilung sortiert, ist der weitere Aufbau des Baumes, folgt man weiter konsequent dem Huffman-Algorithmus, eindeutig. Hätte man in unserem Beispiel im ersten Schritt des Algorithmus die Buchstaben I und S vertauscht, was wegen der gleichen Häufigkeit ihres Auftretens im zu codierenden Text möglich wäre, so bekäme man zwar zu einem anderen Baum. Der Weg dorthin wäre aber wieder eindeutig. An dem Grad der Komprimierung hätte sich allerdings nichts geändert. (Man prüfe dies als Übung). Es lässt sich beweisen, dass diese Art der Komprimierung nach Huffman optimal ist.

Wie man leicht einsehen kann, dient der Huffman-Baum nicht nur der Kodierung sondern auch der Dekodierung. Übersendet man also mittels Huffman-Algorithmus komprimierte Zeichenkette, so muss man dem Empfänger den Kodierungsbaum mitschicken, damit er die empfange Zeichenkette wieder decodieren also dekomprimieren kann. In der Praxis geschieht dies so, dass man in den sog. Header einer komprimierten Datei den Hufmannbaum schreibt. Das hat natürlich zur Konsequenz, dass das Komprimieren sich erst dann lohnt, wenn der Speichergewinn nicht durch das Mitspeichern des Baum wieder verloren geht. Je größer die Datei ist, um so mehr lohnt die Kompression.

Unter Heranziehen des oben aufgestellten Huffman-Baums wollen wir nun noch zeigen, wie wir den Kode 100110011001110110111 wieder entziffern:
Wir interpretieren die Ziffern O und 1 als Kanten und folgen diesen, bis wir zu einem Blatt kommen. Das ist der Fall, wenn wir dem Pfad 1-0-0 gefolgt sind. Das Blatt das wir so erreicht haben trägt das Zeichen M. Nun starten wir erneut bei der Wurzel des Baums und folgen den Kanten, den die Ziffernfolge unseres codierten Wortes vorgeben. Wir folgen also den Kanten 1-1 und kommen wieder an ein Blatt, das jetzt das Zeichen I trägt.