Komplementdarstellung von Variablen des Typs byte

8.3 Die Darstellung des Typs byte im Rechner

Was ist ein Bit, was ein Byte?

Später werden
wir mehr über Datenmenge erfahren.

Auf die Frage "Regnet es?" gibt es die Antwort "ja" oder "nein". Bei der Frage handelt es sich also um eine sog. ja-nein-Frage. Die Datenmenge, die man bei der Beantwortung einer solchen Frage übermittelt, ist 1 Bit. Ein Bit (1 bit) ist also die kleinste Portion an Datenmengen, die man übertragen, oder auch speichern kann. Sie wird im Computer durch das Setzen von 1 im ja-Fall und der 0 im nein-Fall realisiert. Setzt man 8 Bit einer größeren Einheit zusammen, so nennt man den Wert dieser Datenmenge 1 Byte. Also

8 bit = 1 Byte

In einem Speicher der der einer Datenmenge von 1 Byte Platz bietet, kann man also 8 Zeichen aus dem Vorrat {0,1} ablegen. Ein Datentyp, "dessen Variable" gerade einen Platz von 1 Byte beansprucht, ist das byte. (Man beachte die Unterscheidung in der Groß- und Kleinschreibung). Der Inhalt eines solchen Speichers, also die 8 Zeichen bestehen aus den 0 en und 1 en, kann man als Zahl interpretieren.

[0,1,1,1,0,0,1,1]

Bei dieser Interpretation werden die 1en und 0en als Ziffern im Dualsystem interpretiert. Unsere "Zeichen" lassen sich also wie folgt "verstehen":

0111 0011 also 0*128 + 1*64 + 1*32 + 1*16 + 0*8 + 0*4 + 1*2 + 1*1 = 115

Beim Zahlentyp byte in Java kann man also Zahlen von [0000 0000] bis
[1111 1111] darstellen. Wenn man die am weitesten links stehende Stelle zunächst nicht besetzt, sich dort also eine 0 denkt, kann man Zahlen von 0 [0000 0000] bis 127 [0111 1111] darstellen. Tatsächlich werden Ganzzahlen vom Typ byte so dargestellt. Dem am weitesten links stehenden "bit" kommt nun eine besondere Rolle zu. Ist es gesetzt, steht dort also eine 1, so wird bei der Interpretation die "Zahl", die in den restlichen 7 Speicherzellen steht, auf 1000000 ergänzt. Diese Zahl nennen wir das Komplement. Dieser resultierenden Zahl wird ein "-" Zeichen vorgesetzt. Wie das konkret aussieht soll an drei Beispielen gezeigt werden.

1000 0000	letzte 7 Stellen, also 000 0000 auf 1000 0000 ergänzen.	1000 0000 -000 0000 =1000 0000	1000 0000 steht für 128 da im weitesten links stehenden bist eine 1 steht, wird minus vorgesetzt	-128
1000 0001	letzte 7 Stellen, also 000 0001 auf 1000 0000 ergänzen.	1000 0000 -000 0001 =111 1111	111 1111 steht für 127 da im weitesten links stehenden bist eine 1 steht, wird minus vorgesetzt	-127
1000 0010	letzte 7 Stellen, also 000 0010 auf 1000 0000 ergänzen.	1000 0000 -000 0010 =111 1110	111 1110 steht für 126 da im weitesten links stehenden bist eine 1 steht, wird minus vorgesetzt	-126

Ringdarstellung des Datentyps
Byte

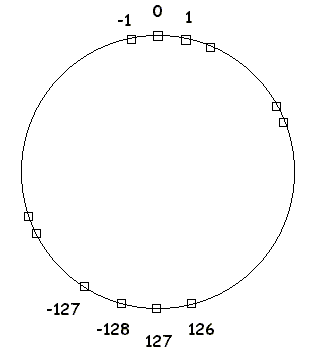Beim Inkrementieren einer Byte - Zahl um 1 (Erhöhen des Zahlenwertes um 1), wird 00000001 addiert, was dem Weiterrücken um eine Stelle in dem Ring (in Uhrzeigersinn) bedeutet. Eine Addition einer beliebigen Zahl kann man sich als ein entsprechend oft ausgeführte Inkrementierung um 1 vorstellen. Dass eine Addition wie (-32)+(40) das richtige Ergebnis liefert, lässt sich an dem links gezeichneten Kreis leicht nachvollziehen. Addiert man zur Zahl 127 eine 1 so wird man als Ergebnis -128 bekommen. (Vgl. dazu die Hausaufgaben). Beim Programmieren muss man also die Tatsache berücksichtigen, dass man leicht zu unsinnigen Ergebnissen kommen kann: 126 + 3 ergibt z.B. -127. Um solche Fehler bei Berechnungen zu vermeiden ist es nötig, sich genau zu überlegen, welchen Datentyp man wählt. Statt den Typ byte kann man short, int oder long wählen. Reicht auch long nicht aus, muss man das Problem mit speziellen Algorithmen lösen, die einen größeren Zahlenbereich simulieren. Was wir hier über die byte- Zahlen gesagt haben gilt natürlich auch für int und long.