|
13.3 Der ggT - Version 3: Rekursiv |
|
| Noch einmal der erweiterte Euklidsche Algorithmus |
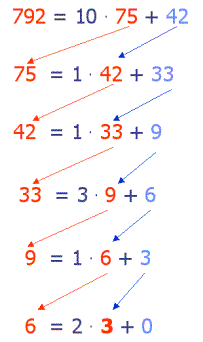 Schauen wir uns noch
einmal den erweiterten Euklidschen Algorithmus an, so wie wir in 12.5
kennen gelernt haben. Ob wir den ggT(792,75) oder den ggT(75,42) berechnen
ist gleich, wir landen immer bei ggT(6,3) und damit bei 3. Das bedeutet
aber nichts anderes, dass wir bei jedem Vorrücken um eine Zeile nach unten
die Berechnung eines ggT zweier Zahlen durch die Berechnung des ggT
einfacherer Zahlen ersetzen. Damit haben wir eine rekursive Formulierung
der Berechnung des ggT zweier Zahlen. Wie einfaches Nachrechnen zeigt,
ersetzen wir beim Zeilenwechsel die Berechnung von Schauen wir uns noch
einmal den erweiterten Euklidschen Algorithmus an, so wie wir in 12.5
kennen gelernt haben. Ob wir den ggT(792,75) oder den ggT(75,42) berechnen
ist gleich, wir landen immer bei ggT(6,3) und damit bei 3. Das bedeutet
aber nichts anderes, dass wir bei jedem Vorrücken um eine Zeile nach unten
die Berechnung eines ggT zweier Zahlen durch die Berechnung des ggT
einfacherer Zahlen ersetzen. Damit haben wir eine rekursive Formulierung
der Berechnung des ggT zweier Zahlen. Wie einfaches Nachrechnen zeigt,
ersetzen wir beim Zeilenwechsel die Berechnung von
ggT(a,b) durch ggT(b,a mod b) wobei a mod b wieder der Rest bei der Division a/b ist. Das alte b wird demnach zum a im nächsten Durchgang und das der Rest (a mod b) wird zum b des nächsten Schritts. Damit der rekursive Abstieg sich nicht im 'unendlichen' verliert, benötigen wir eine Abbruchbedingung, den Basisfall. Den haben wir erreicht, wenn a und b gleich sind, oder wenn b = 0 ist. Der erste Fall tritt eigentlich nur ein, wenn von Anfang an, der ggT zweier gleicher Zahlen bestimmt werden soll. Der Normalfall ist durch die Abbruchbedingung b = 0 ist. Wir sehen das an der letzten Zeile unseres obigen Beispiels. Hier hat a den Wert 6, b den Wert 3 und der Rest (a mod b) ist 0. Da noch keine Abbruchbedingung erfüllt ist kommt es zu dem nächsten Aufruf zur Berechnung des ggTs durch ggT(b, a mod b). Für den nächsten Durchgang ist der erste Parameter (jetzt a) 3 und der zweite 6 mod 3 und damit 0. Die Annruchbedingung ist erreicht, denn der zweite Parameter (jetzt b) ist 0. Der Wert des gesuchten ggT, nämlich 3 ist in a gespeichert, weshalb wir diesen zurückmelden. Eine Javamethode, die den rekursiven Algorithmus implementiert sieht dann so aus:
|
| Schreibtischtest | Ein sog.
Schreibtischtest kann das Arbeiten der Methode verdeutlichen. Wir wählen
dazu drei Szenarien, nämlich die Berechnung von ggT(3,3), also die
Berechnung des ggT zweier gleicher Zahlen, den ggT(24,36) als Vertreter
eines gängigen Beispiels und schließlich ggT(17,19) als Beispiel für die
Berechnung eines ggTs zweier teilerfremden Zahlen, wo wir als ggT-Wert die
1 erwarten. ggT(3,3) =* 3 |
|
Download: GgTTest2.java |
Das
Beispielprogramm zeigt nicht nur das Funktionieren der rekursiven Methode,
es macht auch deutlich, dass man die Methode nicht erst in einer Klasse
wie Mathematik
unterbringen muss um sie zu testen, wir können auch eine Kasse
GgTTest2.java
schreiben, in der die statische Methode
ggT(int
a, int b)
implementiert ist und von der
main-Methode aus aufgerufen
wird. |
|
|
|
| Bemerkungen | Die
Methode ggT(...)
ist außerhalb der main-Methode
implementiert, vergleichbar der Implementierung der Methoden in der Klasse
Mathematik. Der Aufruf erfolgt ohne Punktnotation, da die Klasse dort
implementiert ist, wo sie auch benutzt wird. |
|
Ausgabe
Download: |
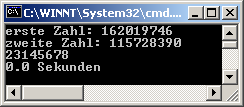 Hat
man sich einmal an rekursive Methode gewöhnt, sind diese häufig einfacher
zu implementieren und zu lesen, als nichtrekursive Methoden.1)
Da, wie die Ausgabe zeigt, die rekursive Methode gegenüber der letzten
Version zur Berechnung des ggT nichts an Effizienz eingebüsst hat,
entscheiden wir uns dafür, die 'ältere' Version der ggT-Methode in der
Klasse Mathematik durch die neuere, die rekursive zu ersetzen. Hat
man sich einmal an rekursive Methode gewöhnt, sind diese häufig einfacher
zu implementieren und zu lesen, als nichtrekursive Methoden.1)
Da, wie die Ausgabe zeigt, die rekursive Methode gegenüber der letzten
Version zur Berechnung des ggT nichts an Effizienz eingebüsst hat,
entscheiden wir uns dafür, die 'ältere' Version der ggT-Methode in der
Klasse Mathematik durch die neuere, die rekursive zu ersetzen.
|
| Fußnote | |
| Es gibt
sogar Algorithmen, die man nur rekursiv formulieren kann, für die wir
keine nichtrekursive Algorithmen finden können. Beispiel dafür ist der
sog. Quicksort-Algorithmus, den wir später noch kennen lernen werden. [zurück] |
|
| zu | 13.4 Fakultät n! |
| zur Startseite | www.pohlig.de (C) MPohlig 2004 |