28.3 Mergesort-Algorithmus
28.3.1 Die Idee des Mergesort-Algorithmus
 
J. v. Neumann

 

 

 

 

 

 

 

 

 

 

mehr zum "von-
Neumann-
Rechner": technische Informatik Uni-Hamburg

 Entwickelt wurde der Mergesort-Algorithmus von John von Neumann (geb. 28.12.1903 in Budapest, Ungarn, gestorben am 08.02.1957 in Washington D.C., USA.). J. v. Neumann war Mathematiker, schrieb als solcher 1932 das Werk "Mathematische Grundlagen der Quantenmechanik" und gilt als einer der Computerpioniere. Er entwarf die Architektur eines Rechner. Die der Architektur zu Grunde liegenden Konzepte gelten heute noch, weshalb man die heutigen Rechner "von Neumann - Rechner" Rechner nennt:

So verlangt die von Neumann - Architektur, dass

  • Programm(kode) und Daten gleichberechtigt im Speicher des Rechners abgelegt werden,
  • ein Programm eine Folge logischer Befehlsentscheidungen ist und
  • bedingende Programmbefehle Entscheidungen über den Fortgang eines Programms erlauben.

Dieses Konzept 'verlang' auch eine entsprechende Architektur auf der Hardwareseite:

  • Eingabegeräte um Daten und Programme in die Maschine eingeben zu können
  • Speicher als Gedächtnis für Daten und Programmanweisungen
  • arithmetische Einheit, um anfallende Berechnungen vornehmen zu können.
  • Leitwerk, um Aufgaben nach Vorgabe eines Programms ausführen zu können.
  • Ausgabegeräte um dem Benutzer über die Ergebnisse von Berechnungen zu informieren.
  1945 entwickelte J. v. Neumann das Konzept für den Mergesort-Algoirithmus. Wie der Quicksort-Algorithmus gehört auch der Mergesort-Algorithmus zu der Klasse der 'divide and conquer'-Algorithmen. Er folgt also auch der Strategie: Teile das Problem. Löse dieses und erzeuge aus den Teillösungen die Gesamtlösung.
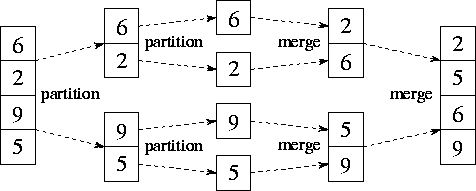
Konkret Zur Veranschaulichung des Algorithmus' gehen wir von einer 4-elementigen Liste aus, die wir in 2 Teillisten zerlegen (partition). Diese werden jeweils in 1 elementige Listen zerlegt. Diese Zerlegung geschieht bei einem rekursiven Abstieg. Beim rekursiven (Wieder)aufstieg werden die Teillisten wieder zusammengmischt (merge). Bei diesem Mischen geschieht das eigentliche Sortieren. Ganz unten, wir haben 1 elemetige Teillisten, sind diese a priori sortiert. Beim Aufstieg wird das Zusammenfügen so organisiert, dass die neu entstehenden, jetzt größeren Teillisten sortiert sind.
   
 
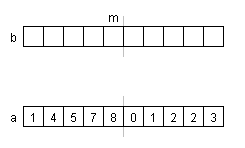
  Wie wir gesehen haben, besteht die eigentliche Sortierarbeit im Zusammenfügen zweier sortierter Listen zu einer neuen, wieder sortierten Liste. Betrachten wir also das Zusammenfügen genauer

Die Situation: Wir sind beim rekursiven Aufstieg und haben unsere Liste a, die zwei sortierte Teillisten enthält. Wir kopieren die Liste in eine Hilfsliste b. Die Position m markiert das am weitesten rechts stehende Element der linken Teilliste.

 
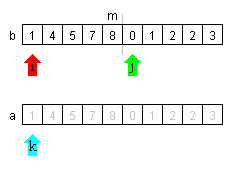
  Wir beginnen mit dem Zusammenfügen. Ziel ist dabei die sortierte Liste a, in der dabei Schritt für Schritte die alten Elemente überschrieben werden. Wir setzen dazu die 'Zeiger' i und k auf das jeweils ersten Plätze der Teillisten. Der Zeiger k zeigt auf ersten Platz der neuen Liste. Der Vergleich der Werte an den Positionen i u´nd k zeigt, dass am Platz k der kleiner Wert steht, der deshalb an die Stelle k der Liste a kopiert wird. Die Zeiger j und k springen um eine Stelle weiter.
 
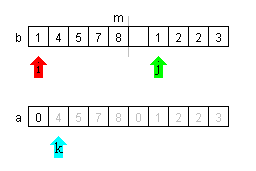
  Jetzt sind die Werte an den Platzen j und k gleich. IN diesem Fall wird der Wert vom Platz i an die Stelle k der Liste a kopiert. Jetzt werden i und k um 1 erhöht.
 
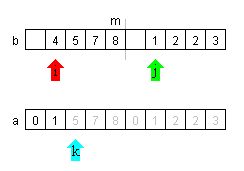
  Der Wert 1 wird nach a kopiert
 
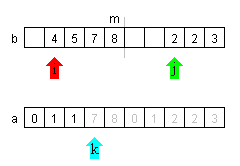
  Der Wert 2 wird nach a kopiert.
 
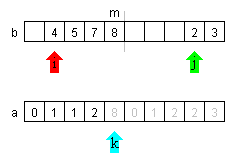
  Dies setzt sich so fort
 
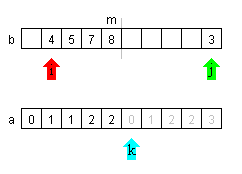
  bis
 
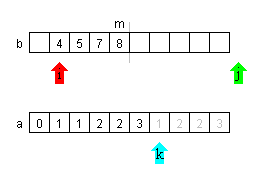
  eine Teilliste leer ist
 
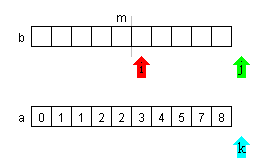
  Da die Teillisten sortiert sind, kann der übrig gebliebene Rest der noch nicht leeren Teilliste auf einen 'Rutsch' in die Liste a kopiert werden
 
zu 28.3.2 Implementierung des Mergesort-Algorithmus
zur Startseite www.pohlig.de  (C) MPohlig 2006