|
6.8.12 Fibonacci-Zahlen |
|
|
|
 Bei dem Versuch
die Populationsentwicklung von Hasen durch ein Modell zu beschreiben fand
Leonardo Pisano, genannt Fibonacci (geb. vermutlich 1170 - gest.
vermutlich 1250; Pisa) die nach ihm benannten Fibonacci Zahlen. War die
Modellierung recht grob, so waren die Zahlen doch von großem Interesse. In
der geometrischen Struktur von Schalentiere, in der Struktur der DNS und
vielem mehr finden sich seine Zahlen immer wieder. Für die Entwicklung der
Mathematik von nicht zu überschätzenden Wert war seine Einführung der
arabischen Ziffern. In der Kunst spielen sie beim Goldenen Schnitt eine
wichtige Rolle. Bei dem Versuch
die Populationsentwicklung von Hasen durch ein Modell zu beschreiben fand
Leonardo Pisano, genannt Fibonacci (geb. vermutlich 1170 - gest.
vermutlich 1250; Pisa) die nach ihm benannten Fibonacci Zahlen. War die
Modellierung recht grob, so waren die Zahlen doch von großem Interesse. In
der geometrischen Struktur von Schalentiere, in der Struktur der DNS und
vielem mehr finden sich seine Zahlen immer wieder. Für die Entwicklung der
Mathematik von nicht zu überschätzenden Wert war seine Einführung der
arabischen Ziffern. In der Kunst spielen sie beim Goldenen Schnitt eine
wichtige Rolle.
Wir können uns diese Zahlen sehr
einfach erzeugt vorstellen. Betrachten Sie dazu die obenstehende
Animation. Wir beginnen mit zwei Quadraten mit der Seitenlänge 1. Zusammen
bilden sie ein Rechteck.
|
| Link informativen Seite | http://www.mcs.surrey.ac.uk/Personal/R.Knott/Fibonacci/fibnat.html |
| zu | 6.8.13 Fibonacci-Zahlen rekursiv bestimmen |
| zur Startseite | www.pohlig.de (C) MPohlig 2005 |

 Über der
längeren Seite des Rechtecks setzen wir ein Quadrat. dessen Seitenlänge
gerade die längere Rechteckseite ist. Gegen den Uhrzeigersinn (man könnte
es auch mit dem Uhrzeigersinn machen) setzen wir das Verfahren fort.
Notieren wir die Folge der Quadratseitenlängen erhalten wir 1; 1; 2; 3; 5;
8; 13; 21; .... Man kann sich die Zahlen auch so erzeugt vorstellen. Man
setzt die ersten beiden Zahlen auf den Wert 1 und die Werte der
nachfolgenden Zahlen erhält man so, dass man die Werte der beiden
jeweiligen Vorgänger addiert: 2 = 1+1; 3 = 2+1; 5 = 3+2; 8 = 5+3 usw. Den
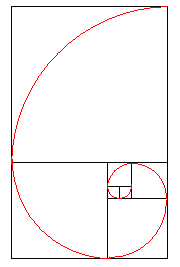
Reiz der in der Animation dargestellten Erzeugung der Fibonacci-Zahlen
erkennt man, wenn man die jeweiligen Quadrate mit einem Viertelkreis
füllt, dessen Radius gerade die Seitenlänge des jeweiligen Quadrates ist.
Es entshet so die sog. Fibonacci-Spirale (siehe links). Diese Struktur
findet sich z.B. bei vielen Gemüsearten oder auch in den Schalen von
Schnecken.
Über der
längeren Seite des Rechtecks setzen wir ein Quadrat. dessen Seitenlänge
gerade die längere Rechteckseite ist. Gegen den Uhrzeigersinn (man könnte
es auch mit dem Uhrzeigersinn machen) setzen wir das Verfahren fort.
Notieren wir die Folge der Quadratseitenlängen erhalten wir 1; 1; 2; 3; 5;
8; 13; 21; .... Man kann sich die Zahlen auch so erzeugt vorstellen. Man
setzt die ersten beiden Zahlen auf den Wert 1 und die Werte der
nachfolgenden Zahlen erhält man so, dass man die Werte der beiden
jeweiligen Vorgänger addiert: 2 = 1+1; 3 = 2+1; 5 = 3+2; 8 = 5+3 usw. Den
Reiz der in der Animation dargestellten Erzeugung der Fibonacci-Zahlen
erkennt man, wenn man die jeweiligen Quadrate mit einem Viertelkreis
füllt, dessen Radius gerade die Seitenlänge des jeweiligen Quadrates ist.
Es entshet so die sog. Fibonacci-Spirale (siehe links). Diese Struktur
findet sich z.B. bei vielen Gemüsearten oder auch in den Schalen von
Schnecken.