Relationen - Graphen (Eine Einführung)
Kreuzprodukt |
Wir geben uns zwei Menge A und B vor, z.B. A = {Hanna, Klara, Rose} und B = {Kurt, David} unter dem Kreuzprodukt von A und B versteht man die Menge aller geordneten Paare (a,b), wobei a aus A und b aus B stammt. In unserem Beispiel wäre das AxB = {(Hanna, Kurt), (Hanna, David), (Klara, Kurt), (Klara, David), (Rose, Kurt), (Rose, David)}. Das geordnet sein drückt sich dadurch aus, dass z.B. das Paar (Kurt, Hanna) nicht Element von AxB sondern von BxA ist. Die Menge A und B können auch Zahlmengen sein und auch beliebig viele Elemente haben: z.B. GxU wenn G die Menge der geraden und U die Menge der ungeraden Zahlen ist. Man schreibe sich von diesem Produkt einige geordnete Paare auf. |
|||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Relation |
Von großem Interesse sind Teilmengen von Kreuzprodukte.
Die Auswahl der Elemente aus dem Kreuzprodukt, die man dann zur Teilmenge zählt kann man sich so vorstellen, dass man ihre Beziehung, ihre Relation beschreibt. Eine Teilmenge aus A x B gewinnt man z.B. dadurch, dass man sagt, welches Mädchen aus A welchen Jungen aus B bei "Damenwahl" zum Tanz auffordert, etwas {(Hanna, Kurt), (Rose, David) (Klara, David)}. Dass dann beim Tanz die Paarungen nicht alle realisiert werden können. ist klar, aber es geht uns nur ums Auffordern. Die besonderen Beziehung, die die Teilmenge definiert, wird in der Frage deutlich, "welches Mädchen fordert welchen Jungen zum Tanz auf?". Dass das Paar (Hanna, Kurt) zur Teilmenge gehört, drückt sich dadurch aus, dass die beiden 'Elemente' Hanna und Kurt in einer besonderen, ausgezeichneten Beziehung oder auch Relation stehen. Die Teilmengen ρ nenne wir auch häufig kurz Relation. Dass das Paar (Hanna, Kurt) zu unserer Teilmenge also zu unserer Relation gehört können wir auch durch Hanna ~ Kurt ausdrücken. (Achtung: manchmal schreibt man auch Hanna ρ Kurt, die ρ-Zeichen werden dann in zwei Bedeutungen benutzt: 1. Es bezeichnet die Teilmenge und 2. es signalisiert, dass ein Paar zur Teilmenge gehört.
|
|||||||||||||||||||||||||
reflexive, ymmetrische transitive Relationen |
Im weiteren betrachten wir noch Relationen, die Teilemenge von AxA sind. Wir nenne eine Relation reflexiv, wenn für alle a aus A gilt a ~ a
|
|||||||||||||||||||||||||
Beispiele |
In NxN geben wir eine Relation "ist Teiler von" vor. Das heißt. Ein geordnetes Paar (a, b) gehört genau dann zur Teilmenge "ist Teiler von" (a ~ b) wenn a Teiler von b ist. z.B. (1, 1), (1, 3), (2, 2), (2, 6), (3, 6) etc. sind Elemente dieser Relation, dagegen (4, 2) nicht. Man kann sich leicht vorstellen, dass diese Relation sowohl reflexiv, denn jede natürliche Zahl teilt sich selbst, und transitiv ist. Sie ist dagegen nicht symmetrisch.
|
|||||||||||||||||||||||||
Äquivalenz-Relation |
Eine Relation heißt Äquivalenzrelation, wenn sie reflexiv, symmetrisch und transitiv ist. Die Gleichheit ist z.B. eine Äquivalenzrelation oder das parallel liegen von Geraden in einer Ebene.
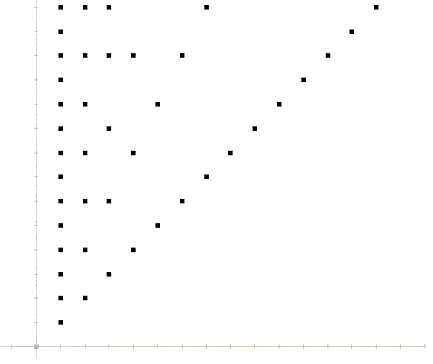
Für das obige Beispiel haben wir A = {1, 2, 3, ... , 13, 14} gewählt und als Relation
wobei a1 ~ a2 wenn a teilt b. Im ersten Moment scheint es etwas schwieriger zu sein, Relationen graphisch darzustellen, wenn die Mengen die beteiligten Mengen keine Zahlen, sondern andere Objekt enthalten. Eine Darstellung der Relation in einem kartesischen Koordinatensystem ist nicht mehr möglich. Man wählt die sog. Graphen. Die Veranschaulichung ist so intuitiv, dass man die Begriffe Graph und Relation identifiziert..
|
|||||||||||||||||||||||||
Knoten und Kanten eines Graphen |
|
|||||||||||||||||||||||||
gewichtete Graphen |
|
|||||||||||||||||||||||||
Darstellung eines Graphen in einem Rechner |
1 -> 2 -> 4 -> ¬ , wobei das ¬-Zeichen zunächst nur sagt, es gibt keine weiteren Verweise. Entsprechend bekommt man Fügen wir alle 4 Zeilen zu einer Liste zusammen und interpretieren wir das ¬ -Zeichen als Trenner, so erhalten wir eine sehr komprimierte Darstellung des Graphen: 1, 2, 4, ¬,2, 3, 4, ¬, 3, 1, ¬, 4, 1, ¬ Eine dritte Variante ist die Darstellung eines Graphen in einer sog. Adjazenzmatrix.
|
|||||||||||||||||||||||||
| Hier sagt die 1 in der Zelle, in der sich in der sich die blau markierte Zeile mit der blau markierten Spalte kreuzt, dass 2 ~ 3. Diese Darstellung ist sehr übersichtlich, benötigt i.A. aber viel Speicher (im Informatik-Alltag muß man von sehr "großen" Graphen ausgehen). | ||||||||||||||||||||||||||
Eigenschaften von Graphen |
gerichtete Kante. Sind alle Kanten im Graphen gerichtet, so sprechen wir von einem gerichteten Graphen |
|||||||||||||||||||||||||
Pfadsuchprobleme |
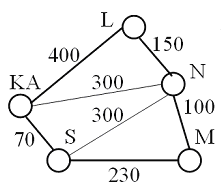
Gesucht ist ein Pfad durch den Graphen, der alle Ort "trifft" und dabei den Weg minimiert. Bekannt ist diese Aufgabe als das Problem eines Handlungsreisenden.
Lässt das Häuschen mit einem Strich zeichnen? Oder anders ausgedrückt, lassen sich alle Knoten so abfahren, dass jede Kante nur einmal benutzt wird? Ein verwandtes Problem zu dieser Aufgabe ist das Königsberger Brückenproblem.
|
|||||||||||||||||||||||||
Eulersche Graphen |
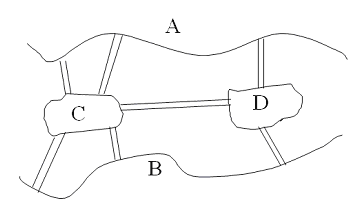
Die "Stadtteile" A, B, C und D der Stadt Königsberg werden durch 7 Brücken miteinander verbunden. Gibt es einen geschlossenen Pfad ( den sog. Eulersche Pfad), der durch alle Teile der Stadt führt, wobei jede Brücke genau einmal passiert wird. Euler |
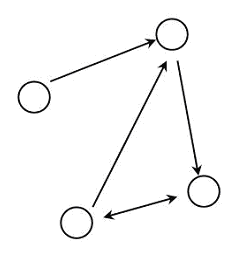Graphen haben Knoten (vertix) und Kanten (edge). Eine Relation ρ als Teilmenge von AxA lässt sich auf einen Graphen abbilden, dabei identifiziert man die Elemente aus der Menge A mit den Knoten des Graphen. Die Tatsache dass a1 ~ a2 gilt, zeigt sich dann darin, dass ein (gerichtete) Kante vom Knoten a1 zum Knoten a2 zeigt. Zeigt die Kante zwischen zwei Knoten in beide Richtungen (manchmal lässt man dann beide Pfeile weg) gilt a1 ~ a2 und a2 ~ a1.
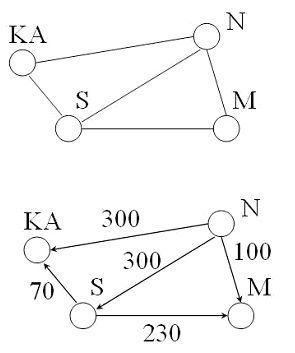Der Graph links oben zeigt eine Relation zwischen den Städten Karlsruhe, Nürnberg, Stuttgart und München. Dabei gilt KA ~ N genau dann, wenn es eine direkte Straßenverbindung zwischen den beiden Städten gibt. Eine solche Relation ist symmetrisch, der Graph deshalb nicht gerichtet. Im nächsten Bild ist der Graph gewichtet, solche Graphen können aber nicht mehr als Relation aufgefasst werden, in der Informatik spielen sie aber eine große Rolle, weshalb sie hier aufgeführt sind. Der Graph drückt aus, dass die Entfernung von Stuttgart nach Karlsruhe nicht unbedingt gleich der Entfernung von Karlsruhe nach Stuttgart sein muss (wenn z.B. wegen einer Baustelle auf der Autobahn, die eine Fahrbahn eine größere Umleitung erfährt).
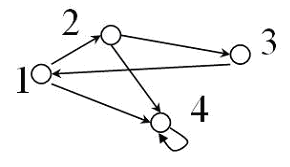Wir geben die Relation durch den neben stehenden Graphen an. Es gibt nun mehrere Möglichkeiten diesen Graphen im Rechner (als Datentyp) darzustellen. Die Menge der Knoten ist A = {1,2,3,4}, die Relation ist gegeben durch die Teilmenge des Kreuzproduktes AxA
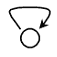reflexive Kante. Besitzen alle Knoten eine reflexive Kante ist die zum Graphen gehörende Relation reflexiv.
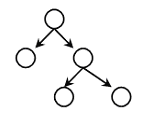Hier ist ein Baum abgebildet. Er besitzt eine Wurzel, das ist ein Knoten, in den keine Kante zeigt. Knoten, von denen keine Kanten mehr ausgehen, heißen Blätter. Gehen von einem Knoten höchstens zwei Kanten aus, sprechen wir von einem Binärbaum. 
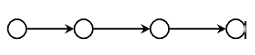Dieser Graph wird Liste genannt, im Rechner wird er häufig als abstrakter Datentyp (auch Liste genannt) realisiert. Sie haben den Vorteil, dass sie zur Laufzeit, also dynamisch, wachsen und schrumpfen können. Entsprechend gilt auch für Bäume. Sie realisieren den abstrakten Datentyp Baum, der wie eine Liste wachsen und schrumpfen kann.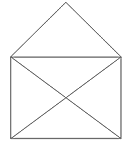 
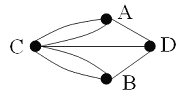hat diese Frage als Graphenproblem behandelt und allgemein gelöst. Betrachten wir zuerst den Graphen, in den sich das Brückenproblem übersetzen lässt.